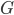Let \(G= \mathbb{Z}_4=\mathbb{Z}/4\mathbb{Z}\) and \(H=\langle2\rangle\) Then \(G= \mathbb{Z}_4 = \mathbb{Z}/4 \mathbb{Z} = \{0,1,2,3\}\).We know \(\mathbb{Z}/4\mathbb{Z}\) is cyclic. Cayley Table of \(G=\mathbb{Z}/4 \mathbb{Z}\) is:\(\begin{array}{|c|c|c|c|c|}\hline\hline\textbf{+} & \textbf{0} & \textbf{1} & \textbf{2} & \textbf{3}\\\hline \textbf{0} & 0 & 1 & 2 & 3 \\\hline \textbf{1} & 1 & 2 & 3 & 0 \\\hline \textbf{2} & 2& 3 & 0 & 1\\\hline\textbf{3} & 3 & 0 & 1 & 2 \\\hline \end{array}\) \(\cong\) \(\begin{array}{|c|c|c|c|c|}\hline\hline\bf{+}…
Tag: Group Theory
Group homomorphism and examples

Group A group is any set G with a defined binary operation (called the group law of \(G\)), written as 2 tuple (examples: \((G,*), (G,\cdot), (G,+), …\)), satisfying 4 basic rules Closure The important point to be understood about a binary operation on \(G\) is that \(G\) is closed with respect to \(*\) in the sense that if \(a,b\in G\) then \(a*b\in G\) (\(a,b\in{C}\) can be read as “a,b element…
A Day out with FreePlane Mindmap and Mathematical Groups

Background I wanted to break away from Blender Learning/Modeling (Current passion) for a day or two. And so I began my exploration in Mathematical Groups using FreePlane Mind mapping software. I had recently switched from Freemind to to Freeplane. There was a simple enough reason for this decision – LaTeX support. Freeplane allows us to enter Mathematical equations using LaTeX. But a certain disadvantage of using Freeplane is that you…