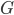Group A group is any set G with a defined binary operation (called the group law of \(G\)), written as 2 tuple (examples: \((G,*), (G,\cdot), (G,+), …\)), satisfying 4 basic rules Closure The important point to be understood about a binary operation on \(G\) is that \(G\) is closed with respect to \(*\) in the sense that if \(a,b\in G\) then \(a*b\in G\) (\(a,b\in{C}\) can be read as “a,b element…
moebiuscurve
Some of my expressions here. (personal blog)