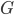Group

A group is any set G with a defined binary operation (called the group law of \(G\)), written as 2 tuple (examples: \((G,*), (G,\cdot), (G,+), …\)), satisfying 4 basic rules

Closure

The important point to be understood about a binary operation on \(G\) is that \(G\) is closed with respect to \(*\) in the sense that if \(a,b\in G\) then \(a*b\in G\)

(\(a,b\in{C}\) can be read as “a,b element of C” or “a,b in C“)

Associativity

\((a*b)*c = a*(b*c), \forall a,b,c\in{G}\)

(\(\forall{a,b}\in{C}\) can be read as “for all a,b in C” or “for all a,b being element of C” or “for each a,b in C” or “for every a,b in C“, …  etc.)

Identity

An element \(e\in G\) (called identity of the Group \(G\)) that satisfies the condition \(e*a=a*e = a, \forall a\in{G}\)

\(G\) contains at most one identity element \(e\)

Inverse

\(\forall a\in{G}\) there exists an element \(a^{-1}\in{G}\) such that \(a*a^{-1} = a^{-1}*a = e\)

Groups can be both finite and infinite.

Some Examples of Group

Example 1

The set \(\mathbb{R}\backslash\{0\}\) (set of all real numbers excluding \(0\)) with the binary operation of multiplication \(((G,*))\)  forms a group.

closure criteria

\(\forall a,b\in \mathbb{R}\backslash\{0\} \implies a*b\in \mathbb{R}\backslash\{0\}\)

For instance,

5*6 =30 is an element of \(R\backslash\{0\}\)

associativity criteria

\(\forall a,b\in \mathbb{R}\backslash\{0\} \implies a*(b*c)= (a*b)*c=a*b*c\)

For instance,

2*(3*9)=(2*3)*9 = 2*3*9=54

identity Criteria

number \(1\) is identity for \(*\) in \(\mathbb{R}\backslash\{0\}\)

\(\forall a\in \mathbb{R}\backslash\{0\}, a*1=1*a=a\)

For instance,

1*5=5*1=5

inverse criteria

\(\forall a\in \mathbb{R}\backslash\{0\} \implies a*a^{-1}=1\)

For instance,

\(2*\frac{1}{2}=2*0.5=1\)

Example 2

The set \(\mathbb{R}\) with the binary operation of addition \(((G,+))\) forms another group

closure criteria

\(\forall a,b\in \mathbb{R} \implies a+b\in \mathbb{R}\)

For instance,

5+6 =11 is an element of \(\mathbb{R}\)

associativity criteria

\(\forall a,b\in \mathbb{R} \implies a+(b+c)= (a+b)+c=a+b+c\)

For instance,

2+(3+9)=(2+3)+9 = 2+3+9=14

identity Criteria

number \(0\) is identity for \(+\) in \(\mathbb{R}\)

\(\forall a\in \mathbb{R}, a+0=0+a=a\)

For instance,

0+5=5+0=5

inverse criteria

\(\forall a\in \mathbb{R}\implies a+a^{-1}=0\)

For instance,

\(2+2^{-1}=2+(-2)=0\)

Subgroup

Given a group \(G\) under a binary operation \(*\), a subset \(H\) of \(G\) is called a subgroup of \(G\) if \(H\) also forms a group under the operation \(*\)

Both Group(\(G\)) and Subgroup(\(H\)) share the same identity \(e\).

Group Table

Group table describes the structure of a finite group by arranging all the possible products of all the group’s elements in a square table (reminiscent of an addition or multiplication table). Many properties of a group – such as whether or not it is abelian, which elements are inverses of which elements, and the size and contents of the group – can be discovered from group table

For group \(G_1=\{1,-1\}\) the multiplication table \(((G_1,*))\) looks like:

For group \(G_2 = \{1, -1, i, -i\}\), the multiplication table \(((G_2,*))\) looks like:

Homomorphism of a Group

if \(G\) and \(H\) are two groups with binary operations \(*\) and \(\circ\), respectively, a function \(f:G\rightarrow{H}\) is a homomorphism if

\(f(a*b)= f(a)\circ{f(b)}\), \(\forall a,b \in{G}\)

Simply put, group homomorphism is a transformation of one Group into another that preserves (invariant) in the second Group the relations between elements of the first.

Examples of Group Homomorphism

Example 1

Let \(G\) be the group of all nonsingular, real, \(N\times{N}\) matrices with the binary operation of matrix multiplication. Let \(H\) be the group \(\mathbb{R} \backslash\{0\}\) with the binary operation of scalar multiplication. The function that is the determinant of a matrix is then a homomorphism from \(G\) to \(H\)

To put this in symbolic context:

Let \((G=\{A,B,C,D,…\},*)\) and let \((H=\mathbb{R}\backslash{\{0\}},\times)\)

Then, \(\det(A*B)=\det(A)\times\det(B)\)

Endomorphism

A homomorphism \(f:G \rightarrow{G}\) is called an endomorphism

Examples of Endomorphism

Example 1

Let \(G\) be the group \(\mathbb{R}\backslash\{0\}\) with the binary operation of multiplication. The function that takes the absolute value of a number is then an endomorphism of \(G\) into \(G\)

To put this in symbolic context:

Let \((G,*)\), \(G=\mathbb{R}\backslash\{0\}\) Then,
\(|x*y|=|x|*|y|\), \(\forall x,y\in{G}\)

For instance,

|-3*4|=|-3|*|4|=3*4=12

And

|-2| = |2|=2

Isomorphism

A homomorphism \(f :G \rightarrow H\) is an isomorphism if \(f\) is both one-to-one and onto (bijective).

Examples of Isomorphism

Example 1

Let \(G\) be the group of positive real numbers with the binary operation of multiplication and let \(H\) be the group of real numbers with the binary operation of addition. The \(\log_b\) function is an isomorphism between \(G\) and \(H\)

To put this in symbolic context:

Let \((G,*)\), \(G ={\{\mathbb{R}^+\}}\) and Let \((H,+)\), \(H={\{\mathbb{R}\}}\),
Then,

\(\log_{b}(x*y) = \log_{b}(x) + \log_{b}(y)\), \(\forall x,y\in{G}\)

(\(\mathbb{R}^+\) denotes set of all positive real numbers)

Automorphism

An isomorphism \(f:G \rightarrow{G}\) is called an automorphism.

Examples of Automorphism

Example 1

Let \(G\) be the group \(\mathbb{R}^+\backslash\{0\}\) with the binary operation of multiplication. The function that takes the absolute value of a number is then an automorphism of \(G\) into \(G\)

To put this in symbolic context:

Let \((G,*)\), \(G=\mathbb{R}^+\backslash\{0\}\), Then, \(|x*y|=|x|*|y|\), \(\forall x,y\in{G}\)

For instance,

[3*4|=|3|*|4|=3*4=12

In this case both sides can use only positive real numbers. Note that this contrasts with an earlier example of Endomorphism where the Group \(G=\mathbb{R}\backslash\{0\}\)

Kernel of Homomorphism

The kernel of a homomorphism \(f:G \rightarrow{H}\) is the subgroup \(f^{-1}(e_0)\) of \(G\).

In other words, the kernel of \(f\) is the set of elements of \(G\) that are mapped by \(f\) to the identity element \(e_0\) of \(H\)

The notation \(K(f)\) can be used to denote the kernel of \(f\)

Examples of Kernel of homomorphism

Example 1

Let \(G\) be the group of all nonsingular, real, \(N \times N\) matrices with the binary operation of matrix multiplication. Let \(H\) be the group \(\mathbb{R}\backslash\{0\}\) with the binary operation of scalar multiplication. The function that is the determinant of a matrix is then a homomorphism from \(G\) to \(H\)

Let \((G=\{A,B,C,D,…\},*)\) and let \((H=\mathbb{R}\backslash{\{0\}},\times)\)
Then,

\(\det(A*B)=\det(A)\times\det(B)\)

In this case the kernel of \(\det\) consists of set of all \(N \times N\) matrices with determinant equal to the real number \(1\)

Example 2

Let \((G,*)\), \(G=\mathbb{R}\backslash\{0\}\), Then,

\(|x*y|=|x|*|y|\), \(\forall x,y\in{G}\)

The kernel of \(|a|, \forall{a}\in{G}\) consists of set \(\{-1,1\}\)

Example 3

Let \((G,*)\), \(G=\mathbb{R}^+\backslash\{0\}\), Then,

\(|x*y|=|x|*|y|\), \(\forall x,y\in{G}\)

The kernel of \(|a|, \forall{a}\in{G}\) consists of set \(\{1\}\)

Example 4

Let \((G,*)\), \(G ={\{\mathbb{R}^+\}}\) and Let \((H,+)\), \(H={\{\mathbb{R}\}}\)

Then,

\(\log_{b}(x*y) = \log_{b}(x) + \log_{b}(y)\), \(\forall x,y\in{G}\)

The kernel of \(\log_b\) is the set \(\{1\}\) because identity \(0\) of \(H\) is mapped to set of all numbers whose \(\log_b\) produces \(0\)

Some simplified theorems derived from homomorphism

(Note: I will not provide any proofs here, because the theorems are quiet simple and proofs can be worked out easily)

Theorem 1

If \(f:G \rightarrow{H}\) is a homomorphism, then \(f(e)\) coincides with the identity element \(e_0\) of \(H\) and \(f(a^{-1}) = f(a)^{-1}\)

Example for Theorem 1

Let \(G\) be the group of all nonsingular, real, \(N\times{N}\) matrices with the binary operation of matrix multiplication. Let \(H\) be the group \(\mathbb{R} \backslash\{0\}\) with the binary operation of scalar multiplication. The function that is the determinant of a matrix is then a homomorphism from \(G\) to \(H\)

To put this in symbolic context:

Let \((G=\{A,B,C,D,…\},*)\) and let \((H=\mathbb{R}\backslash{\{0\}},\times)\)

Then, \(\det(A*B)=\det(A)\times\det(B)\)

In this case the identity of Matrix is the Identity matrix (denoted by \(I\)).

Therefore, \(\det(I*B)= \det(I)\times \det(B)\), where: \(\det(I) =1\) and \(1\) is identity of \(\mathbb{R}\backslash\{0\}\)

Now For \(N=2\), Let \(A = \left[\begin{matrix}2 & 1 \\1 & 2\end{matrix}\right]\)

Then,

\(\det(A)=3\) & \(\det(A)^{-1}=\frac{1}{3}\)

\(A^{-1} = \left[\begin{matrix}\frac{2}{3} & -\frac{1}{3} \\-\frac{1}{3} & \frac{2}{3}\end{matrix}\right]\)

\(\det(A^{-1})=\frac{3}{9}=\frac{1}{3}\)

We can verify that, \(\det(A^{-1})=\det(A)^{-1}\)

Theorem 2

If \(f:G\rightarrow{H}\) is a homomorphism and if \(G’\) is a subgroup of \(G\), then \(f(G’)\) is a subgroup of H

Theorem 3

If \(f:G\rightarrow{H}\) is a homomorphism and if \(H’\) is a subgroup of \(H\) , then the preimage \(f^{-1}(H’)\) is a subgroup of \(G\)

Theorem 4

A homomorphism \(f:G\rightarrow{H}\) is one-to-one if and only if \(K(f) = {e}\).

Theorem 5

If \(f:G\rightarrow{H}\) is an isomorphism, then \(f^{-1}:H\rightarrow{G}\) is an isomorphism

Theorem 6

A homomorphism \(f:G\rightarrow{H}\) is an isomorphism if it is onto and if its kernel contains only the identity element of G.

Group Homomorphism Group Invariant Group Theory