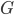(This is a work in progess…) Nth roots of Unity \(n^{th}\) roots of unity is given by the equation:\(\large (1)^{1\over n}=e^{i\frac{2k\pi}{n}}\), \(\large k=0,1,\dots,n-1\) Applet for visualizing nth roots of unity Nth Cyclotomic Polynomial \(n^{th}\) cyclotomic polynomial, for any positive integer \(n\), is the unique irreducible polynomial with integer coefficients that is a divisor of \(x^{n}-1\) and is not a divisor of \(x^{k}-1\) for any \(k < n\). Its roots are…
Useful Propositions of Group Theory

(This is a work in progess…) Rearrangement Theorem: \(R\bf{G} = \bf{G}\) \((\forall R \in \bf{G})\). Equivalent statement about the columns being \(\bf{G} R = \bf{G}\) \((\forall R \in \bf{G})\) Each row and each column in the group multiplication table lists each of the group elements once and only once. From this, it follows that no two elements may be in the identical location in two rows or two columns. Thus,…
Is abelian group \(G\) always isomorphic to H×(G/H)?

Let \(G= \mathbb{Z}_4=\mathbb{Z}/4\mathbb{Z}\) and \(H=\langle2\rangle\) Then \(G= \mathbb{Z}_4 = \mathbb{Z}/4 \mathbb{Z} = \{0,1,2,3\}\).We know \(\mathbb{Z}/4\mathbb{Z}\) is cyclic. Cayley Table of \(G=\mathbb{Z}/4 \mathbb{Z}\) is:\(\begin{array}{|c|c|c|c|c|}\hline\hline\textbf{+} & \textbf{0} & \textbf{1} & \textbf{2} & \textbf{3}\\\hline \textbf{0} & 0 & 1 & 2 & 3 \\\hline \textbf{1} & 1 & 2 & 3 & 0 \\\hline \textbf{2} & 2& 3 & 0 & 1\\\hline\textbf{3} & 3 & 0 & 1 & 2 \\\hline \end{array}\) \(\cong\) \(\begin{array}{|c|c|c|c|c|}\hline\hline\bf{+}…
Some notes on Polynomials

(This is a work in progess…) (Note: I am doing some exploration on Galois Theory and I have written these notes on polynomials here for my own convenience. Please write in the comments section if any clarification is required. Also, I will not provide proofs here for the time being.) Some notations: The symbol \(\mathbb{C}\) is the domain of complex numbers; i.e. set of all possible complex numbers.The symbol \(\mathbb{R}\) is…
Diary – Learning some music

I don’t know anything about music. And I don’t remember how this started, but now I am making an attempt to learn some music using my laptop. Although I never finished this (Hegwid’s Theme), this was 1st piece of music which I programmed after learning to read some sheet music (about a month back). Here’s the part of sheet music, which I used, along with the code. (Click on the…
Diary – fear of move

Doing Art is sometimes more of overcoming fear, hesitations, mental block and other biases that you might have inculcated in you. What you look for is a conceptual space where the (artistic) rules are bendable and it takes a lot of effort to be in that mental conceptual space. And then there is this fear that your Artwork will not be appreciated. But should you care; isn’t art also about…
A review of russian movie konets vechnosti (based on the end of eternity by issac asimov):

There are Eternals and there is Eternity, a temporal field in space-time which exists through centuries. The Eternity was created in the 24th century and does employ best minds from all of the centuries since then. It was supposed to be eternal but beyond a certain future they are blocked by some mysterious power/force. And if they travel beyond these hidden centuries, they find Earth, a barren planet & humanity…
Never assume anything

Knowing my interest in mathematics, a few weeks back, a very close friend of mine, Naveen Balakrishnan, asked me this on WhatsApp- “I’ve an A4 size paper and want to divide it into squares of at least 4cm or more in length with minimal wastage. Is there a mathematical way of solving this than a brute force? All squares should be of equal size” Instinctively after thinking for few minutes,…
Group homomorphism and examples

Group A group is any set G with a defined binary operation (called the group law of \(G\)), written as 2 tuple (examples: \((G,*), (G,\cdot), (G,+), …\)), satisfying 4 basic rules Closure The important point to be understood about a binary operation on \(G\) is that \(G\) is closed with respect to \(*\) in the sense that if \(a,b\in G\) then \(a*b\in G\) (\(a,b\in{C}\) can be read as “a,b element…
My notes on simple Causal Probability

Basic Rules of Probability \(P(A), P(B), …\) represents probability of occurrence of events \(A, B, …\) Probability of any event \(X\) can be calculated as the ratio of the number of chances favorable for event \(X\) to the total number of chances: i.e.; \(P(X) = \frac{m_X}{n}\) where, \(n\) is the total number of chances & \(m_X\) is the number of chances favorable for event \(X\) Probability of any random event lies…